Assignment #10
Reading:
Griffiths, Chapter 9: the following sections:
9.2.1 and 9.2.2 We create electromagnetic waves from Maxwell’s equations. I really want you to revel in the glory of this. See why you needed PHY213 to get here.
9.3.1 but only the first page of it.
9.3.3 This is a lot. Here’s where to concentrate your note-taking:
- The boundary conditions
- See where Snell’s law comes from
- Fresnel’s equations. You’ll use them.
- Understand where Brewster’s angle comes from. You’ll use it.
You may work together and get help from other students. Your solutions must be written in your own words, without looking at someone else’s solutions while you write them.
Don’t forget the 9 points that we are looking for in your solutions (see Moodle).
In order to make sure you get your context and meaning/make sense points, next to your answers, please put a “c” with a circle around it for context, and an “m” with a circle around it for meaning. __________________________
-
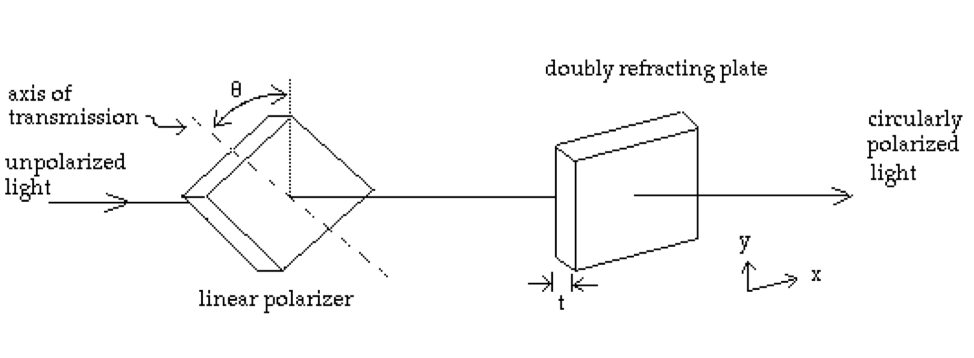
The quarter-wave plate: Some transparent crystals, such as mica or calcite, are doubly refracting; that is, the index of refraction \(n_x\) in the \(\hat{x}\) direction is different than the index of refraction \(n_y\) in the \(\hat{y}\) direction. By placing a linear polarizer in front of a plate of this material, circularly polarized light can be produced by initially unpolarized light. (See figure at bottom.)
If the light has a frequency \(\omega\), for what \(\theta\) and \(t\) (the thickness of the plate) will the emerging beam be circularly polarized? Does it make a difference in which order the two plates are placed?
-
Consider a plane-wave vector field, \(\vec{A}\) , that satisfies the wave equation, i.e. \(\vec{A}\) = \(\vec{A}_0 e^{i(\vec{k}\cdot\vec{r} - \omega t)}\) . Show that
i.) \(\nabla\cdot\vec{A} = i\vec{k}\cdot\vec{A}\)
ii.) \(\nabla\times\vec{A} = i\vec{k}\times\vec{A}\)
iii.) \(k_x^2 + k_y^2 + k_z^2 = \omega^2/c^2\).
- Suppose the critical angle for total internal reflection is 45°. What is the Brewster angle for i.) external reflection and ii) internal reflection?
- Griffiths, Problem 9.17. (Please see hints and an answer below!)
Hints
(#1)
You really just need distance = velocity \(\times\) time. \(t\) will be in terms of \(n_x\) and \(n_y\), \(\omega\), and \(c\). \(\theta\) will be an actual number of degrees.
(#3)
The only place your book talks about total internal reflection is in problem 9.39, although it does do a good job of it. Notice that the only thing that determines that critical angle is the ratio of the two indices of refraction \(n_2/n_1\). So knowing the critical angle is 45\(^\circ\) wil only get you the ratio of the two indices of refraction. Total internal reflection only occurs when the light is going from the higher-index medium into the lower-index medium.
Total external reflection occurs when the incoming light is at grazing incidence to the interface, and is really important in optics in x-ray telescopes. In this case the light goes from the lower index to the higher index.
What the problem is asking you is to solve Brewster’s angle for going from the higher index to the lower-index medium (the total internal reflection case), and for going from the lower-index medium into the higher one (the total external reflection case.) All you need to do for the external reflection case is invert the ratio of \(n_2/n_1\).
(#4)
-
I would draw Figure 9.14 again and add the Electric field on to it. Since the electric field has to be perpendicular to the plane of incidence (otherwise known as your piece of paper) I would choose it coming out of the page in the +y direction. I used \(\theta\) as the incident angle and \(\phi\) as the transmitted angle.
-
Add the magnetic fields to your diagram. You know what direction they must point because the wave travels in the \(\vec{E} x \vec{B}\) direction.
-
Next, use the boundary conditions (9.74) to find the relationships between \(E_T\) \(E_R\) and \(E_I\) and between \(B_T\) \(B_R\) and \(B_I\). You only need the parallel boundary conditions.
-
It’s surprisingly easy to convert the boundary condition on B into another equation for \(E_T\), \(E_R\) and \(E_I\) because amplitude of B is still trivially related to E by \(1/v\) (i.e. \(B = E/v\)). Also, assume that \(\mu = \mu_0\) because actually \(\mu\) doesn’t vary very much in practice. You’ll also need \(\omega = kv\) which is true for waves in general and \(v = c/n\) for electromagnetic waves.
-
Use Snell’s law to find the relationship between \(\theta\) and \(\phi\).
The answer will be this:
\[\tilde{E}_{0R} = \frac{\cos\theta - \sqrt{n^2 - sin^2\theta}}{\cos\theta + \sqrt{n^2 - sin^2\theta}}\tilde{E}_{0I}\] \[\frac{\tilde{E}_{0T}}{\tilde{E}_{0I}} = 1 + \frac{\tilde{E}_{0R}}{\tilde{E}_{0I}}\]where \(n = n_2/n_1\). In other words if the first medium is air, \(n\) is the index of refraction of the 2nd medium.
You may assume: \(\mu_1 = \mu_2 = \mu_0\)
 ]
]