Assignment #5

Reading: Griffiths; Chapter 3, sections 3 and 4.

You may work together and get help from other students. Your solutions must be written in your own words, without looking at someone else’s solutions while you write them.

Don’t forget the 9 points that we are looking for in your solutions (see Moodle).

In order to make sure you get your context and meaning/make sense points, next to your answers, please put a “c” with a circle around it for context, and an “m” with a circle around it for meaning.

1. Griffiths, Chapter 3, Problem 3.16. Replace the question in square brackets with “See if you can come up with a simple way of determining the potential at the center of the cube.”

2. Griffiths, Problem 3.29. This problem is good at giving you intuition about how the multipole expansion is used in practice.

   The next three questions involve solving Laplace’s Equation in cylindrical coordinates.

3. Separate Laplace’s equation in cylindrical coordinates and find three ordinary differential equations in \(s\), \(\phi\), and \(z\). (The \(s\) equation is Bessel’s equation and solutions to it are called Bessel Functions.) Note: this is a little trickier than in Cartesian Coordinates so be careful!

4. Assume that a potential which satisfies Laplace’s equation is independent of the cylindrical coordinate, \(z\).

   (a) Solve the remaining two equations (\(s\) and \(\phi\)) in terms of the separation constant. Hints: Guess a radial function that is a power of \(s\). Also the separation constant in the \(\phi\) equation must be negative. Why?

   (b) Use the fact that you only need a complete set of functions over the interval \(\phi = 0\) to \(2\pi\) to place a condition on the separation constant. (This is what this part used to say…Use the fact that the angular function must be single-valued to place a condition on the separation constant.)

   (c) Using parts (a) and (b), write down the general solution of \(v(s, \phi)\). The terms in the expansion are called cylindrical harmonics. Note: one must treat the case when the separation constant is zero as a separate case. You’ll have to go back to the “\(s\)” equation to get a solution in this case.

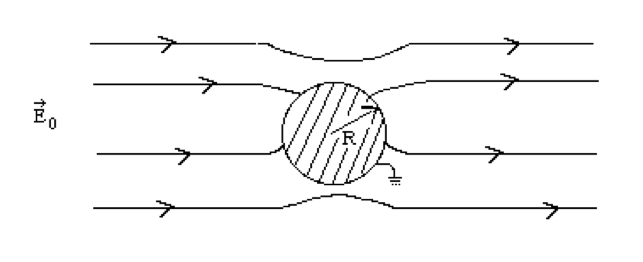
5. Use the expansion in problem 4 to solve the following problem. A long, grounded, cylindrical conductor of radius R is placed in an external, initially uniform electric field \(\vec{E}_0\). The direction of \(\vec{E}_0\) is perpendicular to the axis of the cylinder. Find the potential at points exterior to the cylinder, and also find the charge density on the cylinder.

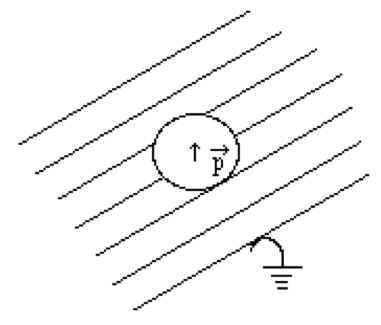
1. Extra problem for fun if you want Suppose a point dipole of strength, \(p\), is placed at the center of a spherical cavity in a grounded conductor. Solve for the potential everywhere in the cavity. Find the charge density on the surface of the cavity.